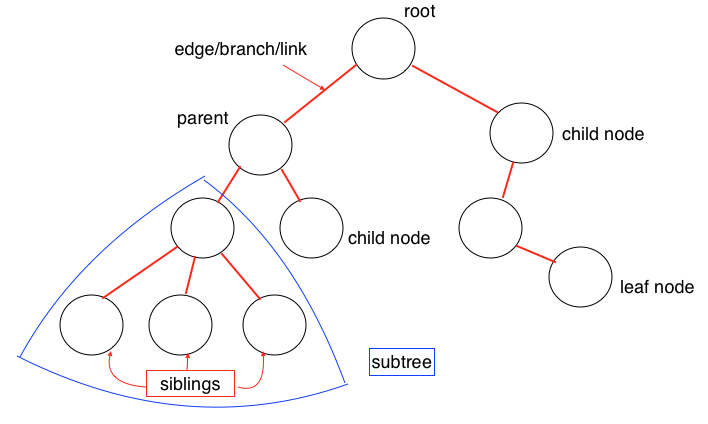
Trees are non-linear data structures that represent nodes connected by edges. Each tree consists of a root node as the Parent node, and the left node and right node as Child nodes.
Monday 28 September 2020
Linked List and Types of Link. Types of Linked List - Singly linked, doubly linked and circular
Linked List and Types of Link
A linked list is a sequence of data elements, which are connected together via links. Each data element contains a connection to another data element in form of a pointer. Python does not have linked lists in its standard library. We implement the concept of linked lists using the concept of nodes as discussed in the previous chapter. We have already seen how we create a node class and how to traverse the elements of a node. In this chapter we are going to study the types of linked lists known as singly linked lists. In this type of data structure there is only one link between any two data elements. We create such a list and create additional methods to insert, update and remove elements from the list.
ListTypes of Linked List - Singly linked, doubly linked and circular.
In this tutorial, you will learn different types of linked list. Also, you will find implementation of linked list in C.
Before you learn about the type of the linked list, make sure you know about the Linked List Data Structure.
There are three common types of Linked List.
- Singly Linked List
- Doubly Linked List
- Circular Linked List
Singly Linked List
It is the most common. Each node has data and a pointer to the next node.
Node is represented as:
struct node {
int data;
struct node *next;
}A three-member singly linked list can be created as:
/* Initialize nodes */
struct node *head;
struct node *one = NULL;
struct node *two = NULL;
struct node *three = NULL;
/* Allocate memory */
one = malloc(sizeof(struct node));
two = malloc(sizeof(struct node));
three = malloc(sizeof(struct node));
/* Assign data values */
one->data = 1;
two->data = 2;
three->data = 3;
/* Connect nodes */
one->next = two;
two->next = three;
three->next = NULL;
/* Save address of first node in head */
head = one;Doubly Linked List
We add a pointer to the previous node in a doubly-linked list. Thus, we can go in either direction: forward or backward.
A node is represented as
struct node {
int data;
struct node *next;
struct node *prev;
}A three-member doubly linked list can be created as
/* Initialize nodes */
struct node *head;
struct node *one = NULL;
struct node *two = NULL;
struct node *three = NULL;
/* Allocate memory */
one = malloc(sizeof(struct node));
two = malloc(sizeof(struct node));
three = malloc(sizeof(struct node));
/* Assign data values */
one->data = 1;
two->data = 2;
three->data = 3;
/* Connect nodes */
one->next = two;
one->prev = NULL;
two->next = three;
two->prev = one;
three->next = NULL;
three->prev = two;
/* Save address of first node in head */
head = one;Circular Linked List
A circular linked list is a variation of a linked list in which the last element is linked to the first element. This forms a circular loop.
A circular linked list can be either singly linked or doubly linked.
- for singly linked list, next pointer of last item points to the first item
- In the doubly linked list, prev pointer of the first item points to the last item as well.
A three-member circular singly linked list can be created as:
/* Initialize nodes */
struct node *head;
struct node *one = NULL;
struct node *two = NULL;
struct node *three = NULL;
/* Allocate memory */
one = malloc(sizeof(struct node));
two = malloc(sizeof(struct node));
three = malloc(sizeof(struct node));
/* Assign data values */
one->data = 1;
two->data = 2;
three->data = 3;
/* Connect nodes */
one->next = two;
two->next = three;
three->next = one;
/* Save address of first node in head */
head = one;Stack introduction
Stack applications in data structure
Following are some of the important applications of a Stack data structure:
- Stacks can be used for expression evaluation.
- Stacks can be used to check parenthesis matching in an expression.
- Stacks can be used for Conversion from one form of expression to another.
- Stacks can be used for Memory Management.
- Stack data structures are used in backtracking problems.
Expression Evaluation
Stack data structure is used for evaluating the given expression. For example, consider the following expression
5 * ( 6 + 2 ) - 12 / 4
Since parenthesis has the highest precedence among the arithmetic operators, ( 6 +2 ) = 8 will be evaluated first. Now, the expression becomes
5 * 8 - 12 / 4
* and / have equal precedence and their associativity is from left-to-right. So, start evaluating the expression from left-to-right.
5 * 8 = 40 and 12 / 4 = 3
Now, the expression becomes
40 - 3
And the value returned after the subtraction operation is 37.
Parenthesis Matching
Given an expression, you have to find if the parenthesis is either correctly matched or not. For example, consider the expression ( a + b ) * ( c + d ).
In the above expression, the opening and closing of the parenthesis are given properly and hence it is said to be a correctly matched parenthesis expression. Whereas, the expression, (a + b * [c + d ) is not a valid expression as the parenthesis are incorrectly given.
Expression Conversion
Converting one form of expressions to another is one of the important applications of stacks.
- Infix to prefix
- Infix to postfix
- Prefix to Infix
- Prefix to Postfix
- Postfix to Infix
- Postfix to Infix
Memory management
The assignment of memory takes place in contiguous memory blocks. We call this stack memory allocation because the assignment takes place in the function call stack. The size of the memory to be allocated is known to the compiler. When a function is called, its variables get memory allocated on the stack. When the function call is completed, the memory for the variables is released. All this happens with the help of some predefined routines in the compiler. The user does not have to worry about memory allocation and release of stack variables.
Consider the following snippet:
int main()
{
// All these variables get memory
// allocated on stack
int f;
int a[10];
int c = 20;
int e[n];
}
The memory to be allocated to these variables is known to the compiler and when the function is called, the allocation is done and when the function terminates, the memory is released.
Backtracking Problems
Consider the N-Queens problem for an example. The solution of this problem is that N queens should be positioned on a chessboard so that none of the queens can attack another queen. In the generalized N-Queens problem, N represents the number of rows and columns of the board and the number of queens which must be placed in safe positions on the board.
The basic strategy we will use to solve this problem is to use backtracking. In this particular case, backtracking means we will perform a safe move for a queen at the time we make the move. Later, however, we find that we are stuck and there is no safe movement for the next Queen, whom we are trying to put on the blackboard, so we have to go back.
This means we return to the queen's previous move, undo this step, and continue to search for a safe place to place this queen.
We will use the stack to remember where we placed queens on the board, and if we need to make a backup, the queen at the top of the stack will be popped, and we will use the position of that queen to resume the search for next safe location.
Hence, stacks can be used for the allocation of memory for most of the backtracking problems.
Stacks and Queues
Stacks and Queues
An array is a random access data structure, where each element can be accessed directly and in constant time. A typical illustration of random access is a book - each page of the book can be open independently of others. Random access is critical to many algorithms, for example binary search.
A linked list is a sequential access data structure, where each element can be accesed only in particular order. A typical illustration of sequential access is a roll of paper or tape - all prior material must be unrolled in order to get to data you want.
In this note we consider a subcase of sequential data structures, so-called limited access data sturctures.
Stacks
| A stack is a container of objects that are inserted and removed according to the last-in first-out (LIFO) principle. In the pushdown stacks only two operations are allowed: push the item into the stack, and pop the item out of the stack. A stack is a limited access data structure - elements can be added and removed from the stack only at the top. push adds an item to the top of the stack, pop removes the item from the top. A helpful analogy is to think of a stack of books; you can remove only the top book, also you can add a new book on the top. A stack is a recursive data structure. Here is a structural definition of a Stack:
it consistes of a top and the rest which is a stack; |  |
Applications
- The simplest application of a stack is to reverse a word. You push a given word to stack - letter by letter - and then pop letters from the stack.
- Another application is an "undo" mechanism in text editors; this operation is accomplished by keeping all text changes in a stack.
Backtracking. This is a process when you need to access the most recent data element in a series of elements. Think of a labyrinth or maze - how do you find a way from an entrance to an exit? Once you reach a dead end, you must backtrack. But backtrack to where? to the previous choice point. Therefore, at each choice point you store on a stack all possible choices. Then backtracking simply means popping a next choice from the stack.
- Language processing:
- space for parameters and local variables is created internally using a stack.
- compiler's syntax check for matching braces is implemented by using stack.
- support for recursion
Implementation
In the standard library of classes, the data type stack is an adapter class, meaning that a stack is built on top of other data structures. The underlying structure for a stack could be an array, a vector, an ArrayList, a linked list, or any other collection. Regardless of the type of the underlying data structure, a Stack must implement the same functionality. This is achieved by providing a unique interface:
public interface StackInterface<AnyType>
{
public void push(AnyType e);
public AnyType pop();
public AnyType peek();
public boolean isEmpty();
}
The following picture demonstrates the idea of implementation by composition.
Another implementation requirement (in addition to the above interface) is that all stack operations must run in constant time O(1). Constant time means that there is some constant k such that an operation takes k nanoseconds of computational time regardless of the stack size.
Array-based implementation
 | In an array-based implementation we maintain the following fields: an array A of a default size (≥ 1), the variable top that refers to the top element in the stack and the capacity that refers to the array size. The variable top changes from -1 to capacity - 1. We say that a stack is empty when top = -1, and the stack is full when top = capacity-1.In a fixed-size stack abstraction, the capacity stays unchanged, therefore when top reaches capacity, the stack object throws an exception. See ArrayStack.java for a complete implementation of the stack class. In a dynamic stack abstraction when top reaches capacity, we double up the stack size. |
Linked List-based implementation
| Linked List-based implementation provides the best (from the efficiency point of view) dynamic stack implementation. See ListStack.java for a complete implementation of the stack class.
|  |
Queues
| A queue is a container of objects (a linear collection) that are inserted and removed according to the first-in first-out (FIFO) principle. An excellent example of a queue is a line of students in the food court of the UC. New additions to a line made to the back of the queue, while removal (or serving) happens in the front. In the queue only two operations are allowed enqueue and dequeue. Enqueue means to insert an item into the back of the queue, dequeue means removing the front item. The picture demonstrates the FIFO access. The difference between stacks and queues is in removing. In a stack we remove the item the most recently added; in a queue, we remove the item the least recently added.
|  |
Implementation
In the standard library of classes, the data type queue is an adapter class, meaning that a queue is built on top of other data structures. The underlying structure for a queue could be an array, a Vector, an ArrayList, a LinkedList, or any other collection. Regardless of the type of the underlying data structure, a queue must implement the same functionality. This is achieved by providing a unique interface.
interface QueueInterface‹AnyType>
{
public boolean isEmpty();
public AnyType getFront();
public AnyType dequeue();
public void enqueue(AnyType e);
public void clear();
}
Each of the above basic operations must run at constant time O(1). The following picture demonstrates the idea of implementation by composition.
Circular Queue
Given an array A of a default size (≥ 1) with two references back and front, originally set to -1 and 0 respectively. Each time we insert (enqueue) a new item, we increase the back index; when we remove (dequeue) an item - we increase the front index. Here is a picture that illustrates the model after a few steps:
As you see from the picture, the queue logically moves in the array from left to right. After several moves back reaches the end, leaving no space for adding new elements
However, there is a free space before the front index. We shall use that space for enqueueing new items, i.e. the next entry will be stored at index 0, then 1, until front. Such a model is called a wrap around queue or a circular queue
Finally, when back reaches front, the queue is full. There are two choices to handle a full queue:a) throw an exception; b) double the array size.
The circular queue implementation is done by using the modulo operator (denoted %), which is computed by taking the remainder of division (for example, 8%5 is 3). By using the modulo operator, we can view the queue as a circular array, where the "wrapped around" can be simulated as "back % array_size". In addition to the back and front indexes, we maintain another index: cur - for counting the number of elements in a queue. Having this index simplifies a logic of implementation.
See ArrayQueue.java for a complete implementation of a circular queue.
Applications
The simplest two search techniques are known as Depth-First Search(DFS) and Breadth-First Search (BFS). These two searches are described by looking at how the search tree (representing all the possible paths from the start) will be traversed.
Deapth-First Search with a Stack
In depth-first search we go down a path until we get to a dead end; then we backtrack or back up (by popping a stack) to get an alternative path.
- Create a stack
- Create a new choice point
- Push the choice point onto the stack
- while (not found and stack is not empty)
- Pop the stack
- Find all possible choices after the last one tried
- Push these choices onto the stack
- Return
Breadth-First Search with a Queue
In breadth-first search we explore all the nearest possibilities by finding all possible successors and enqueue them to a queue.
- Create a queue
- Create a new choice point
- Enqueue the choice point onto the queue
- while (not found and queue is not empty)
- Dequeue the queue
- Find all possible choices after the last one tried
- Enqueue these choices onto the queue
- Return
We will see more on search techniques later in the course.
Arithmetic Expression Evaluation
An important application of stacks is in parsing. For example, a compiler must parse arithmetic expressions written using infix notation:
1 + ((2 + 3) * 4 + 5)*6
We break the problem of parsing infix expressions into two stages. First, we convert from infix to a different representation called postfix. Then we parse the postfix expression, which is a somewhat easier problem than directly parsing infix.
Converting from Infix to Postfix. Typically, we deal with expressions in infix notation
2 + 5
where the operators (e.g. +, *) are written between the operands (e.q, 2 and 5). Writing the operators after the operands gives a postfix expression 2 and 5 are called operands, and the '+' is operator. The above arithmetic expression is called infix, since the operator is in between operands. The expression
2 5 +
Writing the operators before the operands gives a prefix expression
+2 5
Suppose you want to compute the cost of your shopping trip. To do so, you add a list of numbers and multiply them by the local sales tax (7.25%):
70 + 150 * 1.0725
Depending on the calculator, the answer would be either 235.95 or 230.875. To avoid this confusion we shall use a postfix notation
70 150 + 1.0725 *
Postfix has the nice property that parentheses are unnecessary.
Now, we describe how to convert from infix to postfix.
- Read in the tokens one at a time
- If a token is an integer, write it into the output
- If a token is an operator, push it to the stack, if the stack is empty. If the stack is not empty, you pop entries with higher or equal priority and only then you push that token to the stack.
- If a token is a left parentheses '(', push it to the stack
- If a token is a right parentheses ')', you pop entries until you meet '('.
- When you finish reading the string, you pop up all tokens which are left there.
- Arithmetic precedence is in increasing order: '+', '-', '*', '/';
Example. Suppose we have an infix expression:2+(4+3*2+1)/3. We read the string by characters.
'2' - send to the output.
'+' - push on the stack.
'(' - push on the stack.
'4' - send to the output.
'+' - push on the stack.
'3' - send to the output.
'*' - push on the stack.
'2' - send to the output.
Evaluating a Postfix Expression. We describe how to parse and evaluate a postfix expression.
- We read the tokens in one at a time.
- If it is an integer, push it on the stack
- If it is a binary operator, pop the top two elements from the stack, apply the operator, and push the result back on the stack.
Consider the following postfix expression
5 9 3 + 4 2 * * 7 + *
Here is a chain of operations
Stack Operations Output -------------------------------------- push(5); 5 push(9); 5 9 push(3); 5 9 3 push(pop() + pop()) 5 12 push(4); 5 12 4 push(2); 5 12 4 2 push(pop() * pop()) 5 12 8 push(pop() * pop()) 5 96 push(7) 5 96 7 push(pop() + pop()) 5 103 push(pop() * pop()) 515
Note, that division is not a commutative operation, so 2/3 is not the same as 3/2.
Saturday 26 September 2020
Flowchart In Programming
Flowchart In Programming
A flowchart is a diagrammatic representation of an algorithm. A flowchart can be helpful for both writing programs and explaining the program to others.
Symbols Used In Flowchart
| Symbol | Purpose | Description |
|---|---|---|
 | Flow line | Indicates the flow of logic by connecting symbols. |
 | Terminal(Stop/Start) | Represents the start and the end of a flowchart. |
 | Input/Output | Used for input and output operation. |
 | Processing | Used for arithmetic operations and data-manipulations. |
 | Decision | Used for decision making between two or more alternatives. |
 | On-page Connector | Used to join different flowline |
 | Off-page Connector | Used to connect the flowchart portion on a different page. |
 | Predefined Process/Function | Represents a group of statements performing one processing task. |
Examples of flowcharts in programming
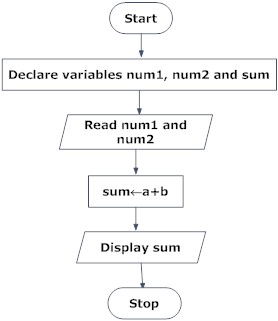
1. Add two numbers entered by the user.
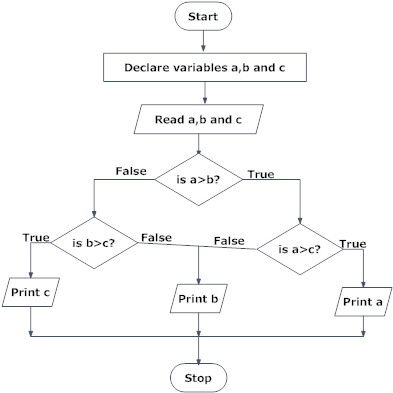
2. Find the largest among three different numbers entered by the user.
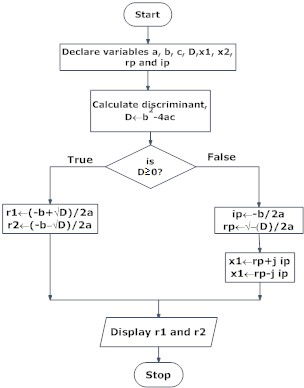
3. Find all the roots of a quadratic equation ax2+bx+c=0
4. Find the Fibonacci series till term≤1000.
Note: Though flowcharts can be useful writing and analysis of a program, drawing a flowchart for complex programs can be more complicated than writing the program itself. Hence, creating flowcharts for complex programs is often ignored.
Flowchart for Addition of Two Matrices....
Flowchart for Addition of Two Matrices
The following Flowchart represents the addition of two matrices.
enter the values of first matrix of size 1 2 3 4 5 6 7 8 9 enter the values of second matrix 9 8 7 6 5 4 3 2 1 addition of two matrix: 10 10 10 10 10 10 10 10 10
Wednesday 16 September 2020
Unit 1 Data structure string definition
Python strings
last modified July 6, 2020
In this part of the Python programming tutorial, we work with string data in more detail.
Python string definition
A string in Python is a sequence of characters. It is a derived data type. Strings are immutable. This means that once defined, they cannot be changed. Many Python methods, such as replace(), join(), or split() modify strings. However, they do not modify the original string. They create a copy of a string which they modify and return to the caller.
Python string literals
Python strings can be created with single quotes, double quotes, or triple quotes. When we use triple quotes, strings can span several lines without using the escape character.
string_literals.py
#!/usr/bin/env python # string_literals.py a = "proximity alert" b = 'evacuation' c = """ requiem for a tower """ print(a) print(b) print(c)
In our example we assign three string literals to a, b, and c variables. And we print them to the console.
$ ./string_literals.py proximity alert evacuation requiem for a tower
Unicode in Python
If we want to create Unicode strings, we add a u or U character at the beginning of the text.
unicode.py
#!/usr/bin/env python # unicode.py text = u'\u041b\u0435\u0432 \u041d\u0438\u043a\u043e\u043b\u0430\ \u0435\u0432\u0438\u0447 \u0422\u043e\u043b\u0441\u0442\u043e\u0439: \n\ \u0410\u043d\u043d\u0430 \u041a\u0430\u0440\u0435\u043d\u0438\u043d\u0430' print(text)
In our example, we print Leo Tolstoy: Anna Karenina in azbuka.
$ ./unicode.py Лев Николаевич Толстой: Анна Каренина
We can use the Russian letters directly if we use the encoding comment.
unicode2.py
#!/usr/bin/python # -*- coding: utf-8 -*- # unicode2.py text = 'Лев Николаевич Толстой: Анна Каренина' print(text)
In this example, we use non-latin characters directly in the source code. We have defined UTF-8 encoding with a encoding comment.
Using quotes in Python
Strings in Python are delimited by single or double quote characters. What if we wanted to display quotes, for example in a direct speech? There are two basic ways to do this.
quotes.py
#!/usr/bin/env python
# quotes.py
print("There are many stars.")
print("He said, \"Which one is your favourite?\"")
print('There are many stars.')
print('He said, "Which one is your favourite?"')
We use the \ character to escape additional quotes. Normally the double quote character is used to delimit a string literal. However, when escaped, the original meaning is suppressed. It appears as a normal character and can be used within a string literal. The second way to use quotes within quotes is to mix single and double quotes.
$ ./quotes.py There are many stars. He said, "Which one is your favourite?" There are many stars. He said, "Which one is your favourite?"
This is the output.
Python string length
The len() method calculates the number of characters in a string. The white characters are also counted.
string_length.py
#!/usr/bin/env python # string_length.py s1 = "Eagle" s2 = "Eagle\n" s3 = "Eagle " print(len(s1)) print(len(s2)) print(len(s3))
We compute the length of three strings.
s1 = "Eagle" s2 = "Eagle\n" s3 = "Eagle "
Three strings are defined. The second string has a new line character at its end. The third has two additional space characters.
print(len(s1))
We print the number of characters to the console.
$ ./length.py 5 6 7
From the output we can see that the white spaces (new line character and space characters in our case) are counted, too.
Python string stripping white characters
In string processing, we might often end up with a string that has white characters at the beginning or at the end of a string. The term white spaces (characters) refers to invisible characters like new line, tab, space or other control characters. We have the strip(), lstrip(), and rstrip() methods to remove these characters.
stripping.py
#!/usr/bin/env python
# strippig.py
s = " Eagle "
s2 = s.rstrip()
s3 = s.lstrip()
s4 = s.strip()
print('{0} {1}'.format(s, len(s)))
print('{0} {1}'.format(s2, len(s2)))
print('{0} {1}'.format(s3, len(s3)))
print('{0} {1}'.format(s4, len(s4)))
We apply the stripping methods on a string word which has three white spaces. One space at the start and two spaces at the end. Note that these methods remove any number of white spaces, not just one.
s2 = s.rstrip()
The rstrip() method returns a string with the trailing white space characters removed.
s3 = s.lstrip()
The lstrip() method returns a string with the leading white space characters removed.
s4 = s.strip()
The strip() method returns a copy of the string with the leading and trailing characters removed.
print('{0} {1}'.format(s2, len(s2)))
The format() method is used to dynamically build a string. The {0} is a control character referring to the first parameter of the format() method. The {1} refers to the second parameter.
$ ./stripping.py Eagle 8 Eagle 6 Eagle 7 Eagle 5
This is the output of the stripping.py example.
Python string escape sequences
When we work with strings, we can use escape sequences. The escape sequences are special characters have a specific purpose, when used within a string.
print(" bbb\raaa") # prints aaabbb
The carriage return \r is a control character for end of line return to beginning of line.
strophe.py
#!/usr/bin/env python
# strophe.py
print("Incompatible, it don't matter though\n'cos someone's bound to hear my cry")
print("Speak out if you do\nYou're not easy to find")
The new line is a control character, which begins a new line of text.
$ ./strophe.py Incompatible, it don't matter though 'cos someone's bound to hear my cry Speak out if you do You're not easy to find
Next we examine the backspace control character.
print("Python\b\b\booo") # prints Pytooo
The backspace control character \b moves the cursor one character back. In our case, we use three backspace characters to delete three letters and replace them with three o characters.
print("Towering\tinferno") # prints Towering inferno
The horizontal tab puts a space between text.
"Johnie's dog" 'Johnie\'s dog'
Single and double quotes can be nested. Or in case we use only single quotes, we can use the backslash to escape the default meaning of a single quote.
If we prepend an r to the string, we get a raw string. The escape sequences are not interpreted.
raw.py
#!/usr/bin/env python # raw.py print(r"Another world\n")
$ ./raw.py Another world\n
We get the string with the new line character included.
Python comparing strings
Comparing strings is a common job in programming. We can compare two strings with the == operator. We can check the opposite with the non-equality != operator. The operators return a boolean True or False.
comparing.py
#!/usr/bin/env python
# comparing.py
print("12" == "12")
print("17" == "9")
print("aa" == "ab")
print("abc" != "bce")
print("efg" != "efg")
In this code example, we compare some strings.
print("12" == "12")
These two strings are equal, so the line returns True.
print("aa" == "ab")
The first two characters of both strings are equal. Next the following characters are compared. They are different so the line returns False.
print("abc" != "bce")
Since the two strings are different, the line returns True.
$ ./comparing.py True False False True False
This is the output.
Python accessing string elements
It is possible to access string elements in Python.
string_elements.py
#!/usr/bin/env python
# string_elements.py
s = "Eagle"
print(s[0])
print(s[4])
print(s[-1])
print(s[-2])
print("****************")
print(s[0:4])
print(s[1:3])
print(s[:])
An index operation is used to get elements of a string.
print(s[0]) print(s[4])
The first line prints the first character. The second line prints the fifth character. The indexes start from zero.
print(s[-1]) print(s[-2])
When the index is negative, we retrieve elements from the end of the string. In this case, we print the last and last but one characters.
print(s[0:4])
Ranges of characters can be accessed too. This line prints a range of characters starting from the first and ending with the fourth character.
print(s[:])
This line prints all the characters from the string.
$ ./string_elements.py E e e l **************** Eagl ag Eagle
This is the output.
A for loop can be used to traverse all characters of a string.
traverse.py
#!/usr/bin/env python # traverse.py s = "ZetCode" for i in s: print(i, " ", end="")
The script prints all the characters of a given string to the console.
$ ./traverse.py Z e t C o d e
This is the output.
Python finding substrings
The find(), rfind(), index() and rindex() methods are used to find substrings in a string. They return the index of the first occurrence of the substring. The find() and index() methods search from the beginning of the string. The rfind() and rindex() search from the end of the string.
The difference between the find() and index() methods is that when the substring is not found, the former returns -1. The latter raises ValueError exception.
find(str, beg=0, end=len(string)) rfind(str, beg=0, end=len(string)) index(str, beg=0, end=len(string)) rindex(str, beg=0, end=len(string))
The str is the substring to be searched for. The beg parameter is the starting index, by default it is 0. The end parameter is the ending index. It is by default equal to the length of the string.
substrings.py
#!/usr/bin/env python
# substrings.py
a = "I saw a wolf in the forest. A lone wolf."
print(a.find("wolf"))
print(a.find("wolf", 10, 20))
print(a.find("wolf", 15))
print(a.rfind("wolf"))
We have a simple sentence. We try to find the index of a substring in the sentence.
print(a.find("wolf"))
The line finds the first occurrence of the substring 'wolf' in the sentence. It prints 8.
print(a.find("wolf", 10, 20))
This line tries to find a 'wolf' substring. It starts from the 10th character and searches the next 20 characters. There is no such substring in this range and therefore the line prints -1, as for not found.
print(a.find("wolf", 15))
Here we search for a substring from the 15th character until the end of the string. We find the second occurrence of the substring. The line prints 35.
print(a.rfind("wolf"))
The rfind() looks for a substring from the end. It finds the second occurrence of the 'wolf' substring. The line prints 35.
$ ./substrings.py 8 -1 35 35
This is the output.
In the second example, we will use the index() and rindex() methods.
substrings2.py
#!/usr/bin/env python
# substrings2.py
a = "I saw a wolf in the forest. A lone wolf."
print(a.index("wolf"))
print(a.rindex("wolf"))
try:
print(a.rindex("fox"))
except ValueError as e:
print("Could not find substring")
In the example, we search for substrings with the index() and rindex() methods.
print(a.index("wolf"))
print(a.rindex("wolf"))
These lines find the first occurrence of the 'wolf' substring from the beginning and from the end.
try:
print(a.rindex("fox"))
except ValueError as e:
print("Could not find substring")
When the substring is not found, the rindex() method raises ValueError exception.
$ ./substrings2.py 8 35 Could not find substring
This is the output of the example.
Python basic string operations
In the next example, we will do string multiplication and concatenation.
add_multiply.py
#!/usr/bin/env python
# add_multiply.py
print("eagle " * 5)
print("eagle " "falcon")
print("eagle " + "and " + "falcon")
The * operator repeates the string n times. In our case five times. Two string literals next to each other are automatically concatenated. We can also use the + operator to explicitly concatenate the strings.
$ ./add_multiply.py eagle eagle eagle eagle eagle eagle falcon eagle and falcon
This is the output of add_multiply.py script.
We can use the len() function to calculate the length of the string in characters.
eagle.py
#!/usr/bin/python # eagle.py var = 'eagle' print(var, "has", len(var), "characters")
In the example, we compute the number of characters in a string variable.
$ ./eagle.py eagle has 5 characters
Some programming languages enable implicit addition of strings and numbers. In Python language, this is not possible. We must explicitly convert values.
string_number.py
#!/usr/bin/python
# string_number.py
print(int("12") + 12)
print("There are " + str(22) + " oranges.")
print(float('22.33') + 22.55)
We use a built-in int() function to convert a string to integer. And there is also a built-in str() function to convert a number to a string. And we use the float() function to convert a string to a floating point number.
Python replacing strings
The replace() method replaces substrings in a string with other substrings. Since strings in Python are immutable, a new string is built with values replaced.
replace(old, new [, max])
By default, the replace() method replaces all occurrences of a substring. The method takes a third argument which limits the replacements to a certain number.
replacing.py
#!/usr/bin/env python
# replacing.py
a = "I saw a wolf in the forest. A lonely wolf."
b = a.replace("wolf", "fox")
print(b)
c = a.replace("wolf", "fox", 1)
print(c)
We have a sentence where we replace 'wolf' with 'fox'.
b = a.replace("wolf", "fox")
This line replaces all occurrences of the 'wolf' with 'fox'.
c = a.replace("wolf", "fox", 1)
Here we replace only the first occurrence.
$ ./replacing.py I saw a fox in the forest. A lonely fox. I saw a fox in the forest. A lonely wolf.
This is the output.
Python splitting and joining strings
A string can be split with the split() or the rsplit() method. They return a list of strings which were cut from the string using a separator. The optional second parameter is the maximum splits allowed.
splitting.py
#!/usr/bin/env python
# splitting.py
nums = "1,5,6,8,2,3,1,9"
k = nums.split(",")
print(k)
l = nums.split(",", 5)
print(l)
m = nums.rsplit(",", 3)
print(m)
We have a comma-delimited string. We cut the string into parts.
k = nums.split(",")
We split the string into eight parts using a comma as a separator. The method returns a list of eight strings.
l = nums.split(",", 5)
Here we split the string into six parts. There are five substrings and the remainder of the string.
m = nums.rsplit(",", 3)
Here we split the string into four parts. This time the splitting goes from the right.
$ ./splitting.py ['1', '5', '6', '8', '2', '3', '1', '9'] ['1', '5', '6', '8', '2', '3,1,9'] ['1,5,6,8,2', '3', '1', '9']
Strings can be joined with the join() string. It returns a string concatenated from the strings passed as a parameter. The separator between elements is the string providing this method.
split_join.py
#!/usr/bin/env python
# split_join.py
nums = "1,5,6,8,2,3,1,9"
n = nums.split(",")
print(n)
m = ':'.join(n)
print(m)
First we split a string into a list of strings. Then we join the strings into one string with the elements being separated by the provided character.
m = ':'.join(n)
The join() method creates one string from a list of strings. The elements are separated by the : character.
$ ./split_join.py ['1', '5', '6', '8', '2', '3', '1', '9'] 1:5:6:8:2:3:1:9
This is the output.
Another method which can be used for splitting strings is partition(). It will split the string at the first occurrence of the separator and return a 3-tuple containing the part before the separator, the separator itself, and the part after the separator.
partition.py
#!/usr/bin/env python
# partition.py
s = "1 + 2 + 3 = 6"
a = s.partition("=")
print(a)
We use the partition() method in this example.
a = s.partition("=")
This will cut the string into three parts. One before the = character, the separator, and the right side after the separator.
$ ./partition.py
('1 + 2 + 3 ', '=', ' 6')
This is the output.
Python string case
Python has four string methods to work with the case of the strings. These methods return a new modified string.
convert_case.py
#!/usr/bin/env python # convert_case.py a = "ZetCode" print(a.upper()) print(a.lower()) print(a.swapcase()) print(a.title())
We have a string word on which we will demonstrate the four methods.
print(a.upper())
The upper() method returns a copy of the string where all characters are converted to uppercase.
print(a.lower())
Here we get a copy of the string in lowercase letters.
print(a.swapcase())
The swapcase() method swaps the case of the letters. Lowercase characters will be uppercase and vice versa.
print(a.title())
The title() method returns a copy of the string, where the first character is in uppercase and the remaining characters are in lowercase.
$ ./convert_case.py ZETCODE zetcode zETcODE Zetcode
This is the output.
Python operations on strings
There are several useful built-in functions that can be used for working with strings.
letters.py
#!/usr/bin/env python
# letters.py
sentence = "There are 22 apples"
alphas = 0
digits = 0
spaces = 0
for i in sentence:
if i.isalpha():
alphas += 1
if i.isdigit():
digits += 1
if i.isspace():
spaces += 1
print("There are", len(sentence), "characters")
print("There are", alphas, "alphabetic characters")
print("There are", digits, "digits")
print("There are", spaces, "spaces")
In our example, we have a string sentence. We calculate the absolute number of characters, number of alphabetic characters, digits and spaces in the sentence. To do this, we use the following functions: len(), isalpha(), isdigit(), and isspace().
$ ./letters.py There are 19 characters There are 14 alphabetic characters There are 2 digits There are 3 spaces
In the next example, we will print the results of football matches.
teams1.py
#!/usr/bin/env python
# teams1.py
print("Ajax Amsterdam" " - " "Inter Milano " "2:3")
print("Real Madridi" " - " "AC Milano " "3:3")
print("Dortmund" " - " "Sparta Praha " "2:1")
We already know that adjacent strings are concatenated.
$ ./teams1.py Ajax Amsterdam - Inter Milano 2:3 Real Madridi - AC Milano 3:3 Dortmund - Sparta Praha 2:1
Next, we will improve the look of the output.
teams2.py
#!/usr/bin/env python
# teams2.py
teams = {
0: ("Ajax Amsterdam", "Inter Milano"),
1: ("Real Madrid", "AC Milano"),
2: ("Dortmund", "Sparta Praha")
}
results = ("2:3", "3:3", "2:1")
for i in teams:
line = teams[i][0].ljust(16) + "-".ljust(5) + teams[i][1].ljust(16) + results[i].ljust(3)
print(line)
The ljust() method returns a left justified string, the rjust() method returns a right justified string. If the string is smaller than the width that we provided, it is filled with spaces.
$ ./teams2.py Ajax Amsterdam - Inter Milano 2:3 Real Madrid - AC Milano 3:3 Dortmund - Sparta Praha 2:1
Now the output looks better.
Python string formatting
String formatting is dynamic putting of various values into a string. String formatting can be achieved with the % operator or the format() method.
oranges.py
#!/usr/bin/env python
# oranges.py
print('There are %d oranges in the basket' % 32)
print('There are {0} oranges in the basket'.format(32))
In the code example, we dynamically build a string. We put a number in a sentence.
print('There are %d oranges in the basket' % 32)
We use the %d formatting specifier. The d character means that we are expecting an integer. After the string, we put a modulo operator and an argument. In this case we have an integer value.
print('There are {0} oranges in the basket'.format(32))
The same task is achieved with the format() method. This time the formatting specifier is {0}.
$ ./oranges.py There are 32 oranges in the basket There are 32 oranges in the basket
The next example shows how to add more values into a string.
fruits.py
#!/usr/bin/env python
# fruits.py
print('There are %d oranges and %d apples in the basket' % (12, 23))
print('There are {0} oranges and {1} apples in the basket'.format(12, 23))
In both lines, we add two format specifiers.
$ ./fruits.py There are 12 oranges and 23 apples in the basket There are 12 oranges and 23 apples in the basket
In the next example, we build a string with a float and a string value.
height.py
#!/usr/bin/env python
# height.py
print('Height: %f %s' % (172.3, 'cm'))
print('Height: {0:f} {1:s}'.format(172.3, 'cm'))
We print the height of a person.
print('Height: %f %s' % (172.3, 'cm'))
The formatting specifier for a float value is %f and for a string %s.
print('Height: {0:f} {1:s}'.format(172.3, 'cm'))
With the format() method, we add f and s characters to the specifier.
$ ./height.py Height: 172.300000 cm Height: 172.300000 cm
We might not like the fact that the number in the previous example has 6 decimal places by default. We can control the number of the decimal places in the formatting specifier.
height2.py
#!/usr/bin/env python
# height2.py
print('Height: %.2f %s' % (172.3, 'cm'))
print('Height: {0:.2f} {1:s}'.format(172.3, 'cm'))
The decimal point followed by an integer controls the number of decimal places. In our case, the number will have two decimal places.
$ ./height2.py Height: 172.30 cm Height: 172.30 cm
The following example shows other formatting options.
various.py
#!/usr/bin/python
# various.py
# hexadecimal
print("%x" % 300)
print("%#x" % 300)
# octal
print("%o" % 300)
# scientific
print("%e" % 300000)
The first two formats work with hexadecimal numbers. The x character will format the number in hexadecimal notation. The # character will add 0x to the hexadecimal number. The o character shows the number in octal format. The e character will show the number in scientific format.
$ ./various.py 12c 0x12c 454 3.000000e+05
The format() method also supports the binary format.
various2.py
#!/usr/bin/python
# various2.py
# hexadecimal
print("{:x}".format(300))
print("{:#x}".format(300))
# binary
print("{:b}".format(300))
# octal
print("{:o}".format(300))
# scientific
print("{:e}".format(300000))
The example prints numbers in hexadecimal, binary, octal, and scientific formats.
The next example will print three columns of numbers.
columns1.py
#!/usr/bin/env python
# columns1.py
for x in range(1, 11):
print('%d %d %d' % (x, x*x, x*x*x))
The numbers are left justified and the output is not optimal.
$ ./columns1.py 1 1 1 2 4 8 3 9 27 4 16 64 5 25 125 6 36 216 7 49 343 8 64 512 9 81 729 10 100 1000
To correct this, we use the width specifier. The width specifier defines the minimal width of the object. If the object is smaller than the width, it is filled with spaces.
columns2.py
#!/usr/bin/env python
# columns2.py
for x in range(1, 11):
print('%2d %3d %4d' % (x, x*x, x*x*x))
Now the output looks OK. Value 2 makes the first column to be 2 charactes wide.
$ ./columns2.py 1 1 1 2 4 8 3 9 27 4 16 64 5 25 125 6 36 216 7 49 343 8 64 512 9 81 729 10 100 1000
Now we have the improved formatting with the format() method.
columns3.py
#!/usr/bin/env python
# columns3.py
for x in range(1, 11):
print('{0:2d} {1:3d} {2:4d}'.format(x, x*x, x*x*x))
Subscribe to:
Posts (Atom)